Iterative Stochastic Elimination Algorithm
Iterative Stochastic Elimination (ISE) is a novel algorithm that was initially developed to solve extremely complex problems in protein structure and interactions. It has since been applied to diverse topics that share a few general "ingredients" and is, therefore, "generic". Problems should involve extremely complex systems of combinatorial nature. Each problem can be presented as a large set of variables in which each variable has very many alternative values (discrete or picked from continuous functions), there is some interdependence of the variables on each other, and there is a scoring function that can evaluate any "configuration" of the system, i.e., any set of variable values that are randomly picked and thus constitutes a "configuration" or "conformation" of the system. A single "sample" constitutes a single random choice of one value for each of the variables. The total number of possible combinations cannot be studied exhaustively as it may be larger than 10100.
Variable values are picked randomly in a broad set of samples that ensures that each variable value would appear enough times to be examined for its effect on the score of each "configuration" in which it appeared. Assuming a variable "A" is a rotatable bond in a protein, which could assume a rotation angle of any value between 0-360 degrees in 1-degree intervals, then a sample of 100,000 will give each of the 360 angles a probability of ~300 to appear in the sample. Such probabilities are the basis for analyzing the large sample, and the analysis allows to make decisions for rejecting some values for each of the variables, thus remaining with a smaller set of potential combinations. The iterations continue until the number of combinations allows them to compute all the remaining options exhaustively and order them by their scores.
Decision making in ISE
The main aim of ISE is to identify those variable values that contribute consistently to the worst results but do not contribute similarly to the best solutions and to eliminate them. This produces a smaller set of variable values and a smaller number of combinatorial options, allowing to proceed to the discovery of a set of optimal states of the system.
A virtual histogram performs the analysis. In that histogram, we identify which of the variable values are consistently associated with the worst scores, and those are rejected from further samplings. This is achieved by focusing only on low and high values in the virtual histogram. Usually 1% at each end of the total number of results, i.e., in a sample of 100,000, we compare each variable value's effect on the results only between the best 1000 and the worst 1000.
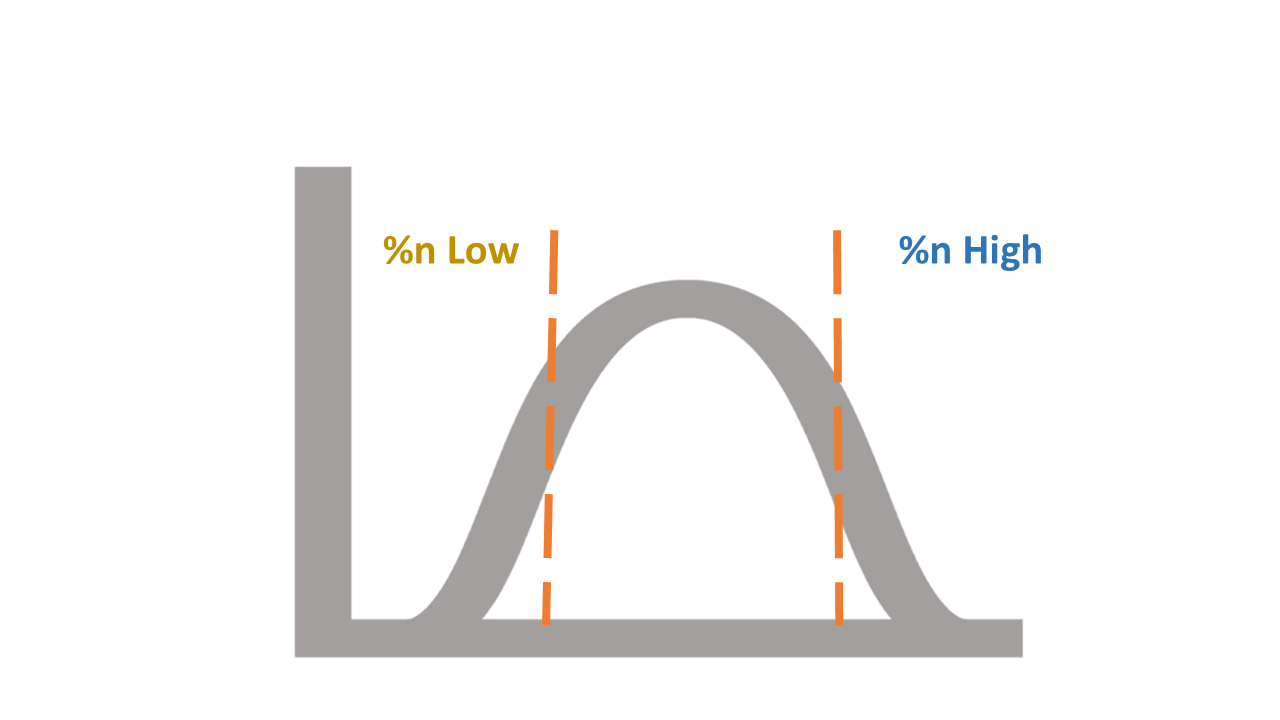
Those values that contribute much more (with statistical significance) to the worst results than the best ones - are marked for elimination. In some applications, they will be eliminated if they also appear as such in subsequent iterations. However, subsequent iterations, therefore, sample a smaller number of combinations than previous iterations. This process continues until the total number of remaining combinations is small enough to perform an exhaustive search of all remaining combinations in reasonable computer time. As this number is in the thousands or millions, we score and sort all of them and obtain a huge set of assumed optimal results, the use of which depends on the application.
ISE Applications
We divide the ISE applications in the field of Drug Discovery into structural studies and classification models. Structural studies require energy evaluations or scoring by energy-related functions such as the closeness of ligand to target residues, closeness to preferred known conformation from a statistical database, H-bonding distances, etc. Classification models score based on previous knowledge, such as correct identification of drugs and non-drugs. In the first application, molecular conformations with various combinations of dihedral angles are built and scored by their energy values. In the second application, filters made of molecular descriptor ranges that distinguish between classes, are constructed and scored by the Matthew's correlation coefficient (MCC) function that accounts for the amount of True and False Negatives and Positives.
ISE for binary classification models
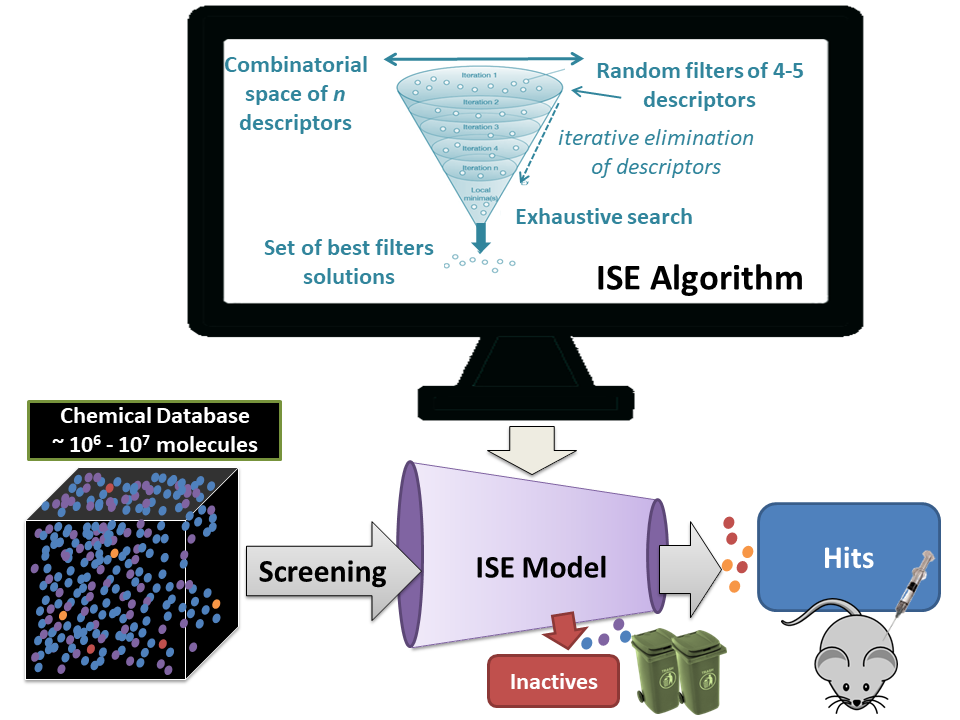
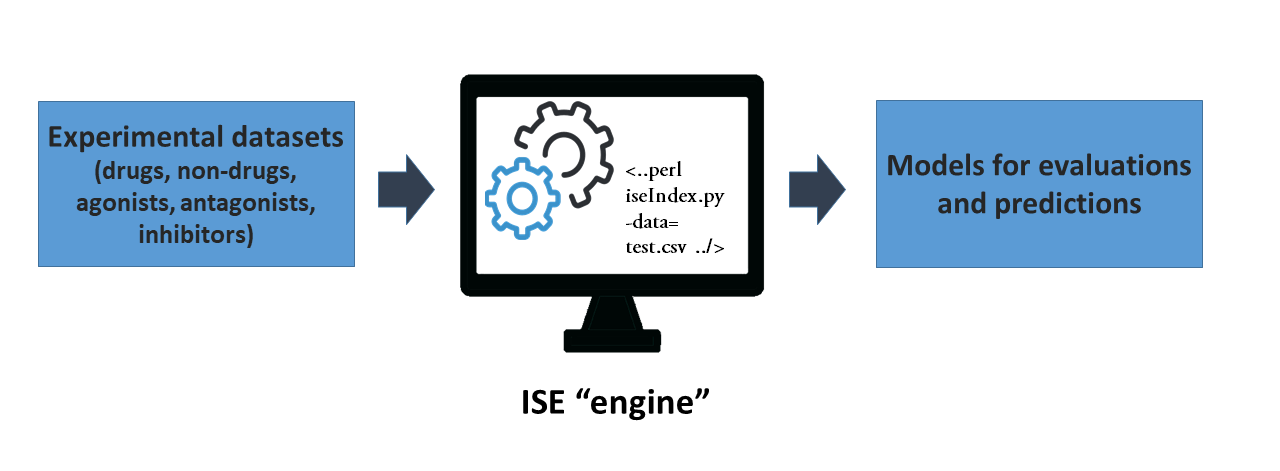
These models can be designed to separate active from inactive molecules for a specific target, highly active compounds from compounds with low activity on a specific or general target, soluble from insoluble compounds, peripheral acting compounds from central nervous system ones, etc. In some cases, it may be easy to classify due to the highly specific nature of the active molecules, but, in general, building such a model is complicated due to the inter-dependence of the molecule's properties one in another. Consequently, optimization is required for many variables simultaneously. The ISE modeling process's main idea is to use some previous data to introduce to the "ISE engine" which produces the models that are subsequently used for evaluations and predictions. This is presented schematically in figure 1:
For classification problems of drugs, databases or other molecular activities sources are used to construct training and test sets. Inactives are picked randomly from a general chemicals database or a commercially available one, assuming the inactivity of molecules that were not measured yet. Molecular properties are computed for all molecules, and ISE is employed to create random combinations of property ranges, which serve as "filters" for classification. Filters are scored by the "Matthews Correlation Coefficient" (MCC) that evaluates a filter's ability to identify positives and negatives correctly, or to misidentify them to be false negatives or false positives, respectively. In equation (1) P = proportion of true Positives, N = proportion of true Negatives Pf and Nf are the proportions of false positives and false negatives, respectively (equation 1).
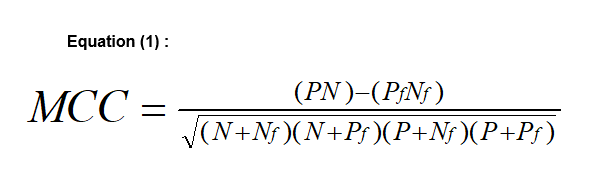
Ranges in filters that contribute consistently to the lowest MCC scores are eliminated, so the number of possible ranges combinations is reduced. The filter creation process, filter scoring, and elimination repeat until a certain low threshold of combinations are reached. From that point, all remaining combinations are scored and sorted. As a result, the ISE process is relatively fast in converging.
Classification models are important in drug discovery and development since they can be used for screening large libraries in a short time and finding candidate molecules as novel actives.
As we get a large number of "filters", each with a different ability to distinguish between Positives and Negatives as reflected in the values of MCC, screening of millions of molecules through these filters is used in order to "index" them by giving a number which is their "Molecular Bioactivity Index" or MBI (equation 2). In equation 2, n is the number of filters, δactive=1 if the molecule passed filter i as a positive, 0 otherwise. δinactive=1 if a molecule passed a filter as a negative, 0 otherwise. P/Pf is the proportion of true to false positives in a particular filter and may be called an "efficiency factor", while N/Nf is an "inefficiency factor", the proportion of true negatives vs. false negatives. Any molecule can obtain a positive number and suggests that it may be a candidate for the particular activity or a negative number that suggests it is not expected to be an active candidate.
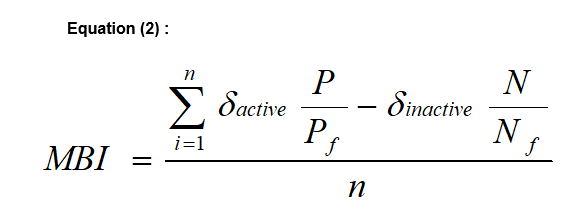
This index can be assigned different names according to the specific molecular bioactivity, such as Drug Like Index (DLI), Cytotoxicity Ratio Index (CRI), hERG toxicity index (ETI), and many others. Figure 2 presents a large molecular dataset screening and the identification of a "focused library" of molecules with a high DLI value that may be drug candidates. Thus, from a starting huge library of molecules, at least more than a million, we finally pick the "top" dozens or more and send them to experimental "wet" validation.
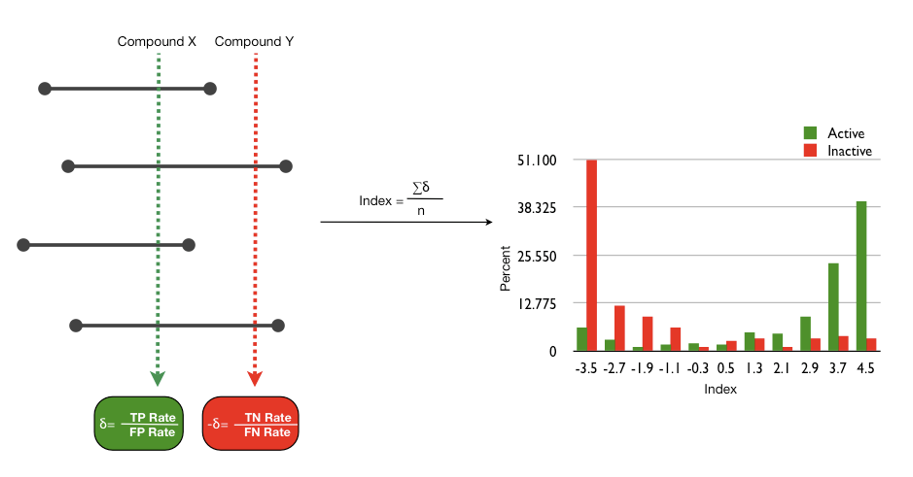
We have already used this approach for many studies of predicting activities in biochemical/pharmacological interactions (i.e., activities measured by thermodynamic constants such as Ki, Kaff, Kd), for pharmacokinetics issues such as solubilities and membrane permeation,for toxicity problems etc. As the ISE process of model construction is relatively fast, it is possible to obtain novel candidates in a very short time.
In all current applications, ISE produces models that help find novel molecular scaffolds that are highly diverse between themselves and with respect to the training sets and have not been previously tested for any biological activity.

